Multiplicative inverse
A number line array pictures how the product of a number and its reciprocal is one(1).
MULTIPLICATIVE INVERSE INSTRUCTIONS
Follow the directions in the dialog box after pressing the <START> button. The <EXPLAIN> button may be pressed to see how to do the example
Two numbers are multiplicative inverses of each other if the product of the numbers is one (1). Multiplicative Inverse is similar to the program Multiply Fractions except that you are to determine the second factor, which will be the multiplicative inverse of the first factor. Another name for multiplicative inverse is reciprocal The following image was made from Multiply with Lines Designer:
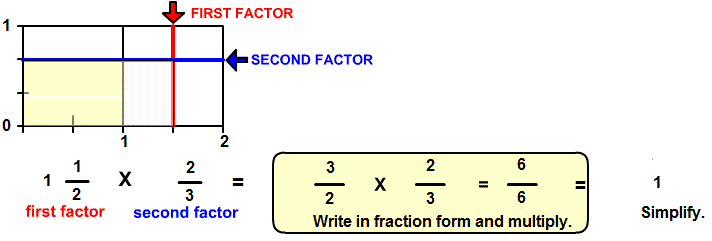
You can see from the picture that the first factor is 1 1/2 units in length. The second factor is the multiplicative inverse or reciprocal of the first factor. To determine the reciprocal, first write the first factor in fraction form as shown in Mixed Numbers to Fraction Form. The answer will be the reciprocal or inverse of the first factor. The numerator of the reciprocal will be the denominator of the first factor. The denominator will be the numerator of the first factor.
In the above example, it is the second factor 2/3 that is the inverse of the first factor. Notice how the numerator 3 in the first factor is written in the denominator of the second factor and the denominator 2 in the first factor is written in the numerator of the second factor.
All the examples in Reciprocal demonstrate that a number multiplied by its inverse gives a product of 1. When you enter the inverse of the first factor correctly, an image of the product 1 will appear in yellow. Also, you will see the numerals for the first factor, the inverse and the product. Reciprocals greater than or equal to 1 may be written in mixed form or in fraction (a/b) form.
You can see from the image of the product that:
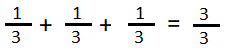
The inverse is the vertical distance, 2/3.
Multiplicative inverse is useful in division of fractions as you will see in the next topic in Visual Fractions, Divide Fractions.
After you enter the fraction form answer you may press the <REPORT> button. The report will ask for your name but you may submit a code for your name. This report will give same results as on the dialog box. The report may be printed or e-mailed.
