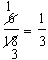Rename to lowest terms with circles
Rename fractions to lowest terms is pictured with circle models.
RENAME TO LOWEST TERMS WITH CIRCLES INSTRUCTIONS
Follow the directions in the dialog box after pressing the <START> button. The <EXPLAIN> button may be pressed to see how to do the example.
Rename to Lowest Terms uses circles to demonstrate how a fraction can be renamed in lowest terms.
The following equivalent fractions were made by Rename to Lowest Terms with Circles Designer :
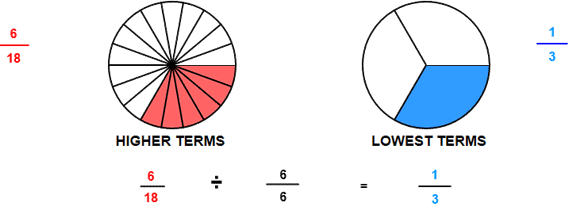
When the program starts, you will see a fraction in higher terms. You are to write the fraction in lowest terms.
To do so, think of the largest number that will divide evenly into both the numerator and the denominator. In the example above, the first fraction has a numerator of 6 and a denominator of 18. The largest number that divides evenly into both 6 and 18 is 6. Six (6) is the greatest common factor of 6 and 18.
The numerator of the second fraction is 1 because 6 divided by 6 is 1.
The denominator of the second fraction is 3 because 18 divided by 6 is 3.
You can see by the illustration that you are actually dividing by 6⁄6, a form of one(1).
After an equivalent fraction in lowest terms is entered, a second circle will appear. The two circles represent the same amount. Although there are less parts in the second circle, the parts are larger, making the two fractions equivalent.
It is important to know that both 6⁄18 and 1⁄3 are equivalent fractions. You are not "reducing" the fraction 6⁄18 by renaming in lowest terms. Some websites and even some textbooks use the term "reduce" but this can cause confusion to many learners.
When renaming 6⁄18 as 1⁄3 you are "writing in lowest terms" or you are " simplifying" 6⁄18.
The fraction on the right is in lowest terms because there is no number larger than 1 that can divide evenly into both the numerator and the denominator.
For more instruction on renaming fractions to lowest terms go to How To Rename to Lower Terms.
After you enter first example you may press the <REPORT> button. This report will give same results as on the dialog box. The report will ask for your name but you may submit a code for your name. The report may be printed or e-mailed.
Another way to write the example is to divide the numerator by the greatest common factor and write the answer over the numerator. Then draw a line through the numerator. Do the same to the denominator, but write the answer under the denominator. This is known as canceling.
See How to Cancel, a short animation on canceling.