Number Properties
Some number system properties
MULTIPLICATIVE INVERSE
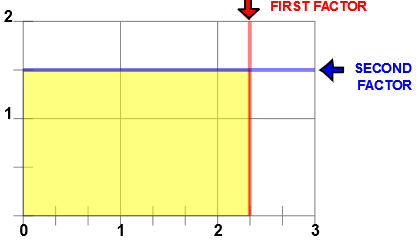
Similarly, 3 x 1/3 = 1

The product of two multiplicative inverses or reciprocals such as 3 and 1/3 is one(1). Input 3 0/1 and 0 1/3 in Multiply with Number Lines to get the above picture. The idea of multiplicative inverse or reciprocal is used in the Divide Fractions with Number Lines page.
COMMUTATIVE PROPERTY OF ADDITION
Similarly, 1 3/4 + 2 1/3 = 2 1/3 + 1 3/4
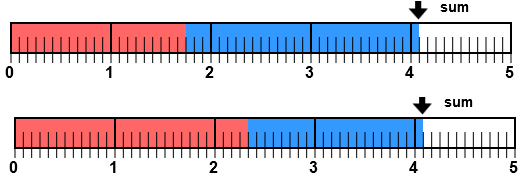
Add Fractions with Number Lines was used to make this image. Input 1 3/4 for the first addend and then 2 1/3 for the second addend. Press the <OK> button to get the number line on top. Then enter 2 1/3 for the first addend and 1 3/4 for the second. After pressing the <OK> button notice that the sum did not change. Only the color patterns for the addends changed.
COMMUTATIVE PROPERTY OF MULTIPLICATION
Similarly, 1 1/3 X 3 = 3 X 1 1/3
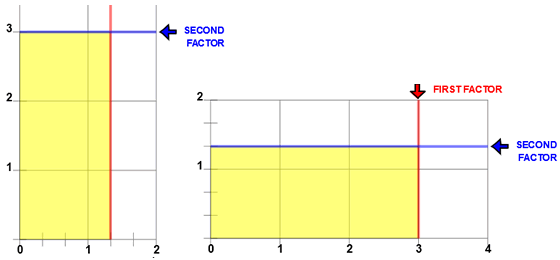
These images were made with Multiplying with Number Lines. Input 1 1/3 for the first factor and 3 0/1 for the second factor. The left image shows 3 rows of 1 1/3. By entering 3 0/1 for the first factor and 1 1/3 for the second factor your product will have 1 1/3 rows of 3. In both cases the product is 4.
DISTRIBUTIVE PROPERTY OF MULTIPLICATION OVER ADDITION
Similarly, 3(2 + 2/5) = (3)(2) + (3)(2/5)
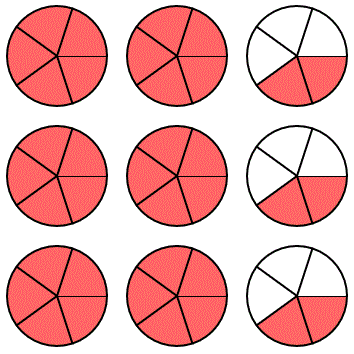
Illustrated are three rows of 2 3/5. The illustration shows 3 rows of 2 circles and 3 rows of (2/5) circles. This gives 6 + 6/5 or 7 1/5 circles.
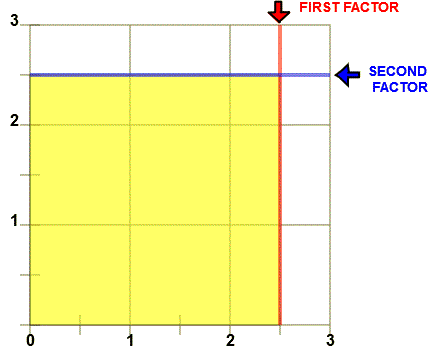
Similarly, (2+1/2) (2+`1/2) = 2x2+2x1/2 +1/2X2+1/2X1/2 = 4 + 1 + 1 + 1/4 = 6 1/4
In algebra class you are taught a short-cut way of multiplying binomials called the FOIL method. FOIL is an acronym to help you remember the short-cut procedure. In FOIL the F in FOIL stands for First, so for (2+1/2)(2+1/2) the first would be 2x2. O stands for Outside so the outside numbers you multiply are 2X1/2. I stands for inside so the two inside numbers are 1/2X2 and L stands for last. The two last numbers are 1/2X1/2. With 2x2+ 2X1/2.+ 1/2X2 + 1/2X1/2 you get 4 + 1 + 1 + 1/4 or 6 1/4. You can see in the picture the 4 wholes, the halves along the top, the halves along the right side, and the 1/4 section.
Try any of these procedures with the below example:
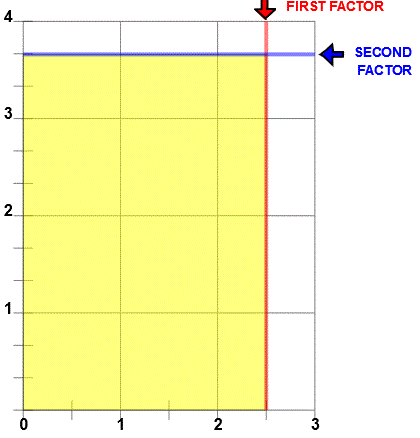
Using the FOIL method for 2 1/2 X 3 2/3 you would write (2+1/2)(3+2/3) = 2X3 + 2X2/3 + 1/2 X 3 + 1/2X2/3 = 6 + 4/3 + 3/2 + 1/3 = 9 1/6. Here, you can see the 6 whole sections, the 4 thirds along the top, the three 1/2 along the right and the 1/3 section in the upper right corner. Not the easiest way to do this example but the picture does show the algebraic connection with multiplying fractions.
The image below was made with Multiplying with Number Lines. 2 1/3 was entered for the first factor and 1 1/2 was entered for the second factor. Can you add the parts of the image to arrive at the product of 3 1/2? See the bottom of the page Multiplying with Number Lines to see the results.