What is Arcsin?

Arcsin, read as “arc sine”, is a notation used to represent the inverse sine function – one of the six inverse trigonometric functions we’ll encounter in trigonometry. Each of the six trigonometric functions will have an inverse function and arcsin is the corresponding function for sine. Thanks to inverse functions like arcsin, we can now work backward, measure unknown angles using their sides, and also establish new properties that will come in handy later on.

In this article, we’ll show you the fundamental definition of arcsin and show you how to evaluate expressions with this function. We’ll also explore its graph, domain, and range to better understand the behavior of inverse sine functions. By the end of our discussion, you’ll feel confident when simplifying and dealing with the function, $y = \arcsin x$ .

The arcsin refers to the inverse function of sine. This means that it reverses the process of evaluating the sine of given angles and returns the angle’s value instead. We can write the inverse sine of $x$ as “ $\arcsin x$ ” or “ $\sin^{-1} x$ ”. What the inverse of sine, $\sin^{-1} x$ , represents are the angles that return $x$ when evaluated by the sine function. However, the function, $\arcsin x$ , represents only the principal value. This difference is important, especially when evaluating values.

This concept is consistent with our definition of inverse functions: when two functions (say $f$ and $f^{-1}$ are said to be each other’s inverses, it should satisfy the condition shown below.

\begin{aligned}f(x) = y &\Rightarrow x = f^{-1}(y)\\\\ \boldsymbol{\sin x = y} &\boldsymbol{\Rightarrow x = \sin^{-1}(y)} \end{aligned}

The arcsin function is no exception – when we reverse the process of $\sin x$ , we simply take its inverse, $\sin^{-1} x$ . Let us show some examples of how the arcsin works given some input values for the inverse sine function.

\begin{aligned}\sin 0 = 0 &\Rightarrow 0 =\sin^{-1} 0\\\sin \dfrac{3\pi}{2} = -1 &\Rightarrow -1 =\sin^{-1} \dfrac{3\pi}{2}\\\sin \dfrac{\pi}{4} = \dfrac{\sqrt{2}}{2} &\Rightarrow \dfrac{\sqrt{2}}{2} =\sin^{-1} \dfrac{\pi}{4}\end{aligned}

These examples highlight the concept of “reversing the process of sine” when evaluating the arcsin of different values. As we have learned from the discussion of inverse functions, the domain and range of inverse functions will, of course, depend on the possible input values for the reference function.

Problem 1

Before we learn more interesting properties of arcsin, it’s time for us to test our understanding first by evaluating the following expressions.

a. $\arcsin \left(\dfrac{1}{2}\right)$

When taking the arcsin of a value, simply think of an angle, $\theta$ , that returns $\dfrac{1}{2}$ when evaluated by the sine function. We’ve learned about special angles in the past, and thankfully, we know that when $\theta = 30\degree$ or $\theta = \dfrac{\pi}{6}$ , its sine value is equal to $\dfrac{1}{2}$ .

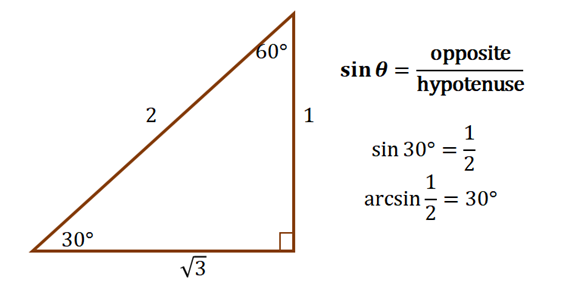
As we have mentioned, arcsin is simply the reverse of the sine function. From this, we have $\arcsin \left(\dfrac{1}{2}\right) = 30\degree$ or $\arcsin \left(\dfrac{1}{2}\right) = \dfrac{\pi}{6}$ .

In the past, we’ve learned that there the sine function is periodic and is not a one-to-one function. This means that there are a lot of angles that return $\dfrac{1}{2}$ when evaluated with the sine function. When asked for the sine inverse, you can give a general form indicating the angles that return $30\degree$ : $\theta =$

This is what makes arcsin different – we’re only focusing on the principal value which is equal to 30⁰. We normally use the range, $-\dfrac{\pi}{2} \leq \theta \leq \dfrac{\pi}{2}$ for our principal value. Let’s apply what we’ve learned to find evaluate the next item.

b. $\arcsin \left(-\dfrac{\sqrt{2}}{2}\right)$

We know that sine is negative in the second and fourth quadrant but since we’re prioritizing angles between the $-\dfrac{\pi}{2}$ and $\dfrac{\pi}{2}$ . This means that we might be looking for a negative angle for $\arcsin \left(-\dfrac{\sqrt{2}}{2}\right)$ .

Here’s a quick guide you can use when determining whether you’d want a positive or negative angle for the principal value. As we have mentioned, our angle can only lie on the second on the fourth quadrant, so we’re looking at an angle in the fourth angle that fits within our range.

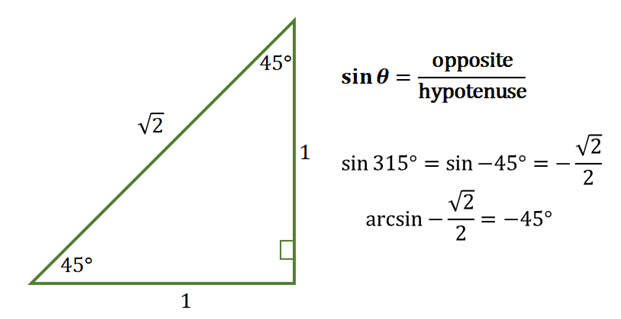
Hence, we have $\arcsin \left(-\dfrac{\sqrt{2}}{2}\right) = -45\degree$ or $\arcsin \left(-\dfrac{\sqrt{2}}{2}\right) = -\dfrac{\pi}{4}\degree$ .

c. $\arcsin \left(0.6\right)$

Of course, there are instances when we’ll need to rely on our handy calculator, graphing device, or even our phones to work on non-special angles. When using the calculator or your calculating device, look for the symbol, $\boxed{\sin^{-1}}$ or $\boxed{\arcsin}$ . Then enter the input value – for our case, it’s 0.6. Hence, we have the following:

\begin{aligned}\sin^{-1} (0.6) &\approx 36.87 \degree\\&\approx 0.64 \text{ radians}\end{aligned}

This means that $\arcsin 0.6$ is approximately equal to 36.87^o and 0.64 radians. Now that we’ve worked on some examples, this gives you more confidence when working with inverse sine and inverse trigonometric functions, in general.

Domain and Range of Arcsin

We’ve studied the domain and range of sine in the past and we know that the sine function is a function with a range of $[-1, 1]$ . We also know that the sine function is not a one-to-one function, we need to restrain the domain of the function within one period such as:

\begin{aligned}\left\{\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right],\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right], \left[\dfrac{\pi}{2}, \dfrac{3\pi}{2}\right],...\right\}\end{aligned}

For each of these intervals, we cover all values of the sine function’s range. Oftentimes, we use the interval, $\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]$ . Now, let’s reverse the sine function’s domain and range to address the arcsin function’s domain and range.

	Domain	Range
$\boldsymbol{\sin x}$	$\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]$	$[-1, 1]$
$\boldsymbol{\arcsin x}$	$[-1, 1]$	$\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]$

This means that the domain of $\arcsin x$ is $[-1, 1]$ and its range is $\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]$ . Knowing the conditions for the arcsin’s domain and range will come in handy when solving equations and graphing inverse sine functions.

Understanding the Graph of Arcsin

We’ve now established the domain and range for arcsin, let’s learn how to graph its parent function. When graphing the curve of $y = \arcsin x$ , use the fact that our range will be limited to $-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$ and the domain will be $[-1, 1]$ .

As we’ve learned when graphing other functions, let’s construct a table of values for $y = \arcsin x$ . Use special angles when graphing $\arcsin x$ ’s curve.

$\begin{aligned}\boldsymbol{x}\end{aligned}$	$\begin{aligned}\boldsymbol{\sin^{-1}x}\, \textbf{in Degrees}\end{aligned}$	$\begin{aligned}\boldsymbol{\sin^{-1}x}\, \textbf{in Radians}\end{aligned}$
$\begin{aligned}-1\end{aligned}$	$\begin{aligned}-90\degree\end{aligned}$	$\begin{aligned}-\dfrac{\pi}{2}\end{aligned}$
$\begin{aligned}-\dfrac{\sqrt{3}}{2}\end{aligned}$	$\begin{aligned}-60\degree\end{aligned}$	$\begin{aligned}-\dfrac{\pi}{3}\end{aligned}$
$\begin{aligned}-\dfrac{\sqrt{2}}{2}\end{aligned}$	$\begin{aligned}-45\degree\end{aligned}$	$\begin{aligned}-\dfrac{\pi}{4}\end{aligned}$
$\begin{aligned}-\dfrac{1}{2}\end{aligned}$	$\begin{aligned}-30\degree\end{aligned}$	$\begin{aligned}-\dfrac{\pi}{6}\end{aligned}$
$\begin{aligned}0\end{aligned}$	$\begin{aligned}0\degree\end{aligned}$	$\begin{aligned}0\end{aligned}$
$\begin{aligned}\dfrac{1}{2}\end{aligned}$	$\begin{aligned}30\degree\end{aligned}$	$\begin{aligned}\dfrac{\pi}{6}\end{aligned}$
$\begin{aligned}\dfrac{\sqrt{2}}{2}\end{aligned}$	$\begin{aligned}45\degree\end{aligned}$	$\begin{aligned}\dfrac{\pi}{4}\end{aligned}$
$\begin{aligned}\dfrac{\sqrt{3}}{2}\end{aligned}$	$\begin{aligned}60\degree\end{aligned}$	$\begin{aligned}\dfrac{\pi}{3}\end{aligned}$
$\begin{aligned}1\end{aligned}$	$\begin{aligned}90\degree\end{aligned}$	$\begin{aligned}\dfrac{\pi}{2}\end{aligned}$

Take note of these special values to help you when solving equations involving the arcsin. For now, let’s use some of the values and graph their points on the xy-coordinate system. Connect the points to sketch the curve of our function, $y = \arcsin x$ as shown below.

This curve confirms that the arcsin satisfies the definition of inverse functions. If you include the sine function’s curve, you’ll see that the graph of $y= \sin^{-1} x$ is simply the reflection of $y = \sin x$ ’s curve with respect to the line, $y = x$ .

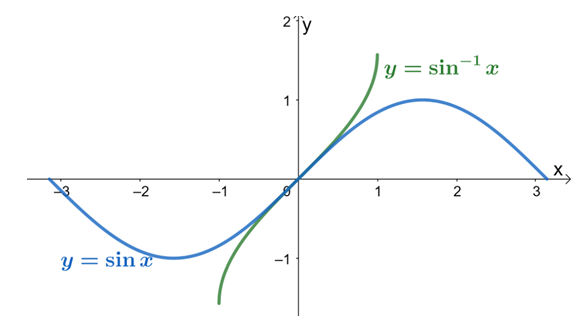
We’ve now explored all the fundamentals we need to know about arcsin, so in the last part of our discussion, we’ll show you different applications of the inverse sine function. This will also make you appreciate the concept behind inverse trigonometric functions as well.

What Are Some Applications of Arcsin?

We can use our knowledge of inverse sine functions when finding unknown angle measures. We’ll also need arcsin to find unknown values from equations that involve the sine function. Whenever we need to reverse the process of sine functions, we’ll be using $\arcsin$ or $\sin^{-1}$ .

\begin{aligned} y &= \sin x\\x&= \sin^{-1} y\end{aligned}

When given special ratios, you can use special angles or triangles to find unknown values. Keep your calculating device with you though because we’ll need it for some of the examples.

Problem 2

A ladder is leaning against the wall and forms an angle, $\theta$ , with the ground. If the wall is 4 meters high and the ladder is 5 meters long, what is the value of $\theta$ ?

Sketch a right triangle to illustrate the problem and help you know what these values represent in the context of a right triangle.

We can relate the angle, $\theta$ , to the side opposite it and the hypotenuse, so we have $\sin \theta = \dfrac{4}{5}$ .To find the measure of the angle, we’ll be using the arcsin function.

\begin{aligned} \sin \theta &= \dfrac{4}{5}\\\arcsin \left(\sin \theta\right) &= \arcsin \left(\dfrac{4}{5}\right)\\\theta &= \arcsin \dfrac{4}{5} \end{aligned}

Use your calculating device to approximate the value of $\theta$ .

\begin{aligned}\theta &\approx 53.13\degree \end{aligned}

This means that the ladder forms an angle of approximately 53.13^o with the ground.

Problem 3

Solve the equation, $30 \sin (10x) – 10 = 5$ .

First, let’s isolate $\sin (10x)$ on the left-hand side of the equation.

\begin{aligned} 30 \sin (10x) - 10 &= 5\\30\sin(10x) &= 15\\\sin (10x) &= \dfrac{1}{2}\end{aligned}

Now, to find the value of $10x$ , we simply take the inverse sine to reverse the process of evaluating $10x$ using the sine function. This means that we’ll take the arcsin of both sides of the equation.

Use the fact that $\sin 30\degree = \dfrac{1}{2}$ to find the value of $x$ .
For the left-hand side of the equation, use the fact that $f^{-1}[f(x)] =x$ , so $\arcsin(\sin x) = x$ .

Hence, we can simplify the equation as shown below.

\begin{aligned} \arcsin[\sin (10x) ]&= \arcsin\left(\dfrac{1}{2}\right)\\10x &= 30\degree\\x &= 3\degree\end{aligned}

Thanks to the inverse sine function, we can now solve equations like this. In fact, we have $x = 3\degree$ .

What Is Arcsin?