The angle of elevation and knowing how to find its measure are important topics in trigonometry. It is formed between an observer’s line of sight when looking up and the horizontal distance between the object and the observer. Through the angle of elevation, we can easily establish the relationship between the vertical and horizontal distances of an object from an observer’s eye.
Trigonometric ratios are essential when working on word problems involving angle of elevation, so this article is also a refresher on how to use these ratios in word problems. This article covers all the key concepts needed to master this topic and you’ll be given different examples to work on so you can also test your understanding!
What Is Angle of Elevation?
The angle of elevation is the angle formed between the horizontal line and a given observer’s line of sight. From its name, the angle of elevation represents the angle formed by the ground or base and the direction or the observer’s line of sight as the observer looks up at an object. Thus, the name of this special angle – angle of elevation deals with angles formed from an elevated line of sight or when a given observer looks up.
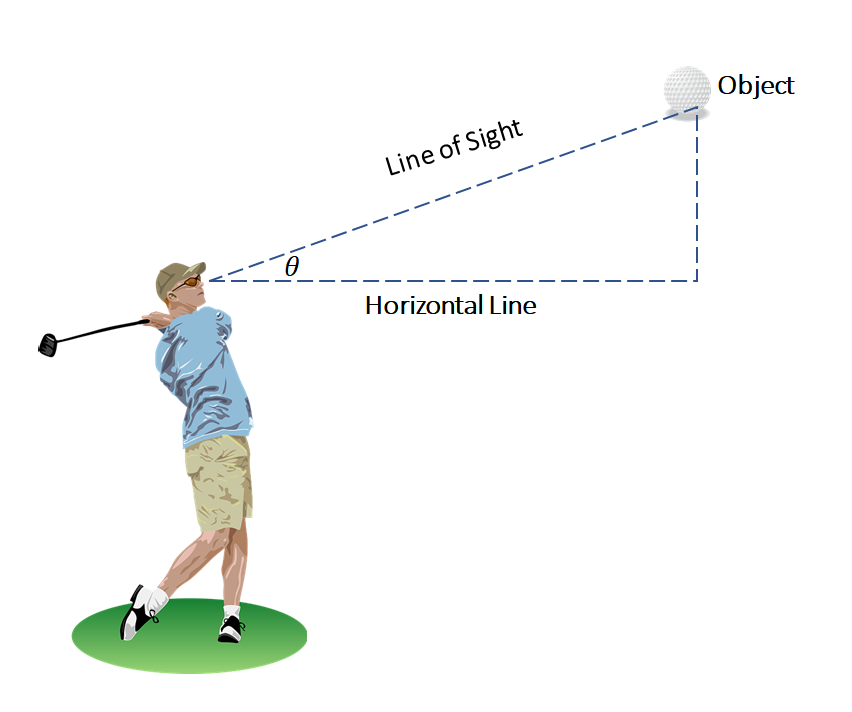
We’ve been throwing around the words, line of sight, horizontal line, and object, so to better understand the fundamentals of the angle of elevation, take a look at the image shown above. The man has putt a golf ball causing it to travel along the direction elevated from his perspective.
- The line of sight describes the direction that which an observer is looking at the object. For the angle of elevations, lines of sight are always elevated from the observer’s eyes.
- The horizontal line is an imaginary used to guide us in measuring the horizontal distance of the observer from the final distance reached by the object.
- The angle, \theta, is formed by these two lines acting as the angle’s arrays. These two lines are connected by the object’s height from the horizontal base to form a right triangle.

This means that given an observer at A and an observer at C as shown above, a right triangle is formed using the following segments:
- The segment connecting the observer’s line of sight, (\overline{AC}).
- The distance between the object from the horizontal base (\overline{BC}).
- The segment that highlights the horizontal distance between the observer and the object, (\overline{AB}).
The angle of elevation, \theta, is formed by the two lines: the horizontal line (\overline{AB}) and the line of sight (\overline{AB}). Now that we’ve established a right triangle that contains the angle of elevation, the relationship between the angle of elevation and the line segments’ ratios can be established.
Problem 1
To use the angle of elevation in word problems, it’s important to set up the right triangle and assign the appropriate values. As a warm-up, construct a diagram that illustrations the description below:
A girl is observing a kite being flown with an angle of elevation of 45o. The kite is 12\sqrt{2} ft away from the girl’s line of sight and is 12 ft above the ground.
When setting up a right triangle that illustrates a situation or a word problem, remember that the angle of elevation lies between the line of sight and the horizontal distance between the observer and the object. Suppose that \overline{AB} represents the line of sight and \overline{BO} represents the horizontal distance. Form a right triangle with \overline{AB} and \overline{AO} form the angle of elevation, 45o.

This diagram highlights the situation clearly – the girl looks at the kite with an angle of elevation of 45o. The line of sight (\overline{AB}) is 12\sqrt{2} feet away and the height of the kite from the girl’s eye level (\overline{BO}) is 12 feet.
This is an important exercise because word problems involving angles of elevation normally require an initial illustration as a guide. In the next section, we’ll cover the fundamental trigonometric relationships that can be observed from the angle of elevation and the corresponding right triangle’s sides. Through trigonometry, problems involving angle of elevation and line of sight can easily be solved by applying key properties.
How To Use Trigonometry in Angle of Elevation?
To use trigonometry in solving problems involving angle of elevation, set up the key relationships shared between the angle of elevation and the right triangle’s sides. Since right triangles are involved, learn how to set up the important trigonometric ratios to solve for unknown measures.
When working with angles of elevation and the corresponding right triangle, identify the sides opposite and adjacent to the angle of elevation. The line of sight represents the hypotenuse of the right triangle.

Now, use past lessons to set up different trigonometric ratios that are helpful for a particular problem. The formulas below summarize the relationships shared between the triangle’s sides and the three trigonometric ratios: \sin \theta, \cos \theta, and \tan \theta.
\begin{aligned}\sin \theta = \dfrac{o}{h} &\Rightarrow \theta = \sin^{-1} \left(\dfrac{o}{h}\right)\\\cos\theta = \dfrac{a}{h} &\Rightarrow \theta = \cos^{-1} \left(\dfrac{a}{h}\right)\\\tan\theta = \dfrac{o}{a} &\Rightarrow \theta = \tan^{-1} \left(\dfrac{o}{a}\right)\end{aligned}Depending on what’s given, use the appropriate trigonometric ratio to solve for the unknown measures. Before diving into a word problem involving angle of elevation, practice applying these trigonometric ratios first by answering the problem below.
Problem 2
Using the trigonometric ratios, find the measures of \theta and h for each of the right triangles. Round off their measures to two decimal places.

Working on the first triangle, the object’s height and its distance from the observer are given. From the angle of elevation, these are sides opposite and adjacent to it, respectively. To find the angle of elevation’s measure, use tangent since \tan \theta represents the ratio between these two sides’ lengths.
\begin{aligned}\tan \theta &= \dfrac{o}{a}\\\tan \theta&= \dfrac{15}{27}\\\theta&= \tan\left( \dfrac{15}{27}\right)\\&\approx 29.06\degree\end{aligned}a. From this, we can see that the angle of elevation is approximately equal to 29.06o.
Now, apply a similar process to solve for h from the second triangle. This time, the angle of elevation’s measure and line of sight’s distance are given while the object’s height is unknown. Use \sin 30\degree then equate it to the ratio of the object’s height and the observer’s line of sight.
\begin{aligned}\sin \theta &= \dfrac{o}{h}\\\sin 30\degree &= \dfrac{h}{15}\\\dfrac{1}{2}&= \dfrac{h}{15}\\h&= \dfrac{15}{2}\\&=7.50\end{aligned}b. Hence, the object’s height is equal to 7.50 cm.
When working with a word problem that involves the angle of elevation, illustrate the problem with a right triangle then apply appropriate trigonometric formulas to solve for the unknown measures. The process will then be similar to the ones we’ve just shown you, so when ready, try out the word problems that follow!
Problem 3
Alexis is biking around her campus when she noticed that a dormitory’s rooftop has a lot of potted sunflowers. She was 50 feet away from the dormitory when she was looking up to notice and appreciate the sunflowers. If the rooftop’s distance from the second floor is 24 feet, what was the angle of elevation’s measure?
First, illustrate a problem to fully understand how the given lengths and angle of elevation relate to each other. The object (sunflowers)’s height and the horizontal distance (Alexis’ distance from the dormitory) are given.

The angle of elevation, \theta, is opposite to the sunflower and rooftop’s height and adjacent to the given horizontal distance. The most efficient way to solve for \theta is by using \tan \theta to relate these two lengths. Use a graphing device or any online software to estimate the value of \theta to two decimal places.
\begin{aligned}\tan \theta &= \dfrac{o}{a}\\\tan \theta&= \dfrac{24}{50}\\\theta&= \tan\left( \dfrac{24}{50}\right)\\&\approx 25.64\degree\end{aligned}This shows that Alexis was looking at the potted sunflowers from an angle of elevation of 25.64o.
Problem 4
While sailing his boat at night, John looked up and saw the nearest lighthouse’s lights. The distance between the lighthouse’s top and his boat’s base is 46 feet. The angle of elevation is 25o from John’s line of sight. What is the horizontal distance between John’s boat and the nearby lighthouse’s base?
As always, begin by illustrating the problem to help guide you in solving for the unknown lengths. The right triangle below represents the distance between John’s boat and the lighthouse – with the line of sight measuring 46 feet.

Since the line of sight’s distance and angle of elevation are given, the best trigonometric function to choose is sine this time. This shows that although most problems involving angle of elevation use tangent most of the time, it’s still important to double-check and find simpler solutions.
Now, equate \cos 25\degree to the ratio of the unknown distance, a, and the line of sight’s distance. Solve for a to find the horizontal distance between John’s boat and the lighthouse.
\begin{aligned}\cos \theta &= \dfrac{a}{h}\\\cos 25\degree &= \dfrac{a}{46}\\a &= 46\cos 25\degree\\&\approx 41.69\end{aligned}This means that John’s boat is approximately 41.69 feet away from the lighthouse.
Conclusion
Hopefully, this article has helped you to understand what the angle of elevation is and how you can use trigonometry to use it in everyday life, as with the example problems above.
