Adjacent angles are important pairs of angles you’ll be studying in basic and advanced geometry. You may also have encountered objects that form adjacent angles such as slices of pizzas, steering wheels, and even the clock. You’ll learn why these objects are at adjacent angles by reading this article!
In this article, you’ll learn about the conditions that all adjacent angles have to meet. We’ll also show you the important properties to know about adjacent angles. By the end of this discussion, we want you to feel confident when working on different applications of adjacent angles.
What Are Adjacent Angles?
Adjacent angles are pairs of angles that share a common side and share a common vertex. It is important to note that for two angles to be adjacent, their angles must never overlap. Imagine two angles being merged together to form a larger angle as can be seen from the figure shown below.
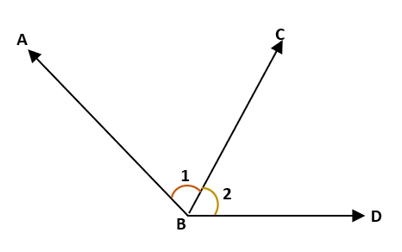
Let’s take a look at the two adjacent angles,\angle ABC and \angle CBD, that form the larger obtuse angle, \angle ABD.
- The two adjacent angles share a common vertex, B.
- They also share a common side, \overline{BC}.
- The two angles also do not overlap each other and only meet at the vertex.
By inspection alone, we can immediately see whether two angles are adjacent to each other. Can you think of real-world examples that contain adjacent angles or are adjacent angles themselves? Here are some common examples you might think of:
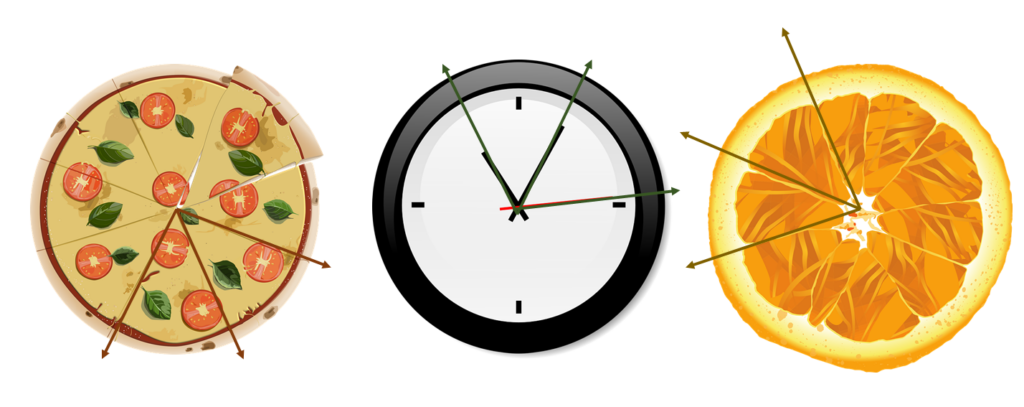
- Two slices of pizzas lying beside each other form adjacent angles – with the center as the common vertex.
- The hands of the clock can form adjacent angles at the right time. With the second, minute, and hour hands forming the angles as shown above.
- Slices of oranges, like slices of pizzas, do form adjacent angles as well when they’re lying beside each other.
We’ve now covered the definition of adjacent angles and also shown some real-world examples. You might also have heard angles inside a polygon being referred to as adjacent angles, so it’s important that we highlight the difference between these two.
Understanding Adjacent Angles in Polygons
When given a polygon and its interior angles, adjacent angles in this context simply mean the angles lying next to each other. These adjacent interior angles will still share a common side.

For example, in this hexagon, C and D, are adjacent interior angles simply because they share a common side, \overline{CD}. We just wanted to clarify that when working with adjacent angles in polygons, we’re simply looking at angles that lie next to each other. Don’t confuse this definition with adjacent angles formed by two or more angles. Let’s now resume our discussion of adjacent angles and a great way to do so is to try a warm-up problem first!
Problem 1
Determine whether the following statements are true or false based on our definition of adjacent angles. Use the diagram shown below when necessary.
a. The angles \angle ABC and \angle DBE are adjacent angles and share a common point of B.
It’s true that the two angles, \angle ABC and \angle DBE, share a common point or vertex of B. However, by a closer look, the two angles do not share a common side. This is a crucial condition for two angles to be adjacent, so the statement is false.
b. The angles \angle ABC and \angle CBD are adjacent angles and share a common side of \overline{BC}.
From the diagram, we can see that the two angles share a common vertex and a common side (BC).
This means that the two angles satisfy the definition of adjacent angles, so the statement is indeed true.
c. The sum of \angle CBD and \angle CDE is equal to \angle CBE.
The two angles are adjacent – they share a common side of \overline{BD} and a common vertex of B. Now, these two adjacent angles form a larger angle as can be seen from the diagram. When combined together, \angle CBD and \angle CDE form the larger angle, \angle CBE.
This means that the sum of the two angles is equal to the measure of \angle CBE. Hence, the statement is true. At this point, we know you want to know more interesting facts and properties about adjacent angles. This is why the next section covers all the properties and common types of adjacent angles you’ll encounter in basic geometry.
What Are Some Properties and Common Examples of Adjacent Angles?
Adjacent angles are distinct because of the common side and vertex they share. Here are some other interesting properties about adjacent angles:
- The adjacent angles will never overlap each other – keep this in mind all the time as well.
- Since they will never overlap, a pair of adjacent angles will never share a common interior point.
- It is possible for adjacent angles to be complementary or supplementary. Below are examples of complementary and supplementary adjacent angles.
- We know that adjacent angles share a common side. Here’s another property: adjacent angles must also have a non-common side!
These are important facts to remember about adjacent angles. We’ve covered a solid base for adjacent angles, so let’s use our current knowledge to answer the problems below.
Problem 2
Write down five pairs of adjacent angles from the diagram shown below.

When looking for pairs of adjacent angles, make sure that they satisfy the two main conditions first: 1) they share a common vertex and 2) they share a common side. By observing the diagram, we can see that we can find adjacent angles by using O as the common point.
Let’s first focus on the upper half of the diagram – we can see that aside from the shared vertex, O, the angles \angle AOB and COB share a common side: \overline{OB}. This means we have our first pair of vertical angles: \angle AOB and \angle COB.
On the lower half, we can see that there are two pairs of adjacent angles. Each pair will share a common side of \overline{OD} and O will remain the common vertex. Hence, our second and third pairs of adjacent angles are:
- \angle COD and \angle ODE
- \angle ODE and \angle EOA
For the last two pairs of adjacent angles, let’s look at the right and left sides of the diagram.
Hence, we have the last two pairs of adjacent angles:
- \angle COD and \angle COB (common side of \overline{CO}katex])</li><li>[katex]\angle BOA and \angle AOE (common side of \overline{OA}katex])</li></ul>
<p>When looking for adjacent angles from a large diagram or from multiple angles, it helps to look for them in a structured way like we’ve shown you. This helps you from making sure all pairs are accounted for and to avoid duplicating any pair of adjacent angles from your list. </p>
<p>Now, let’s zoom in on adjacent angles that are complementary and supplementary since they open a wide range of applications for us later on in more advanced math topics.</p>
<h2 class="wp-block-heading">Understanding Complementary and Supplementary That Are Adjacent Angles</h2>
<p>Complementary and supplementary angles are angles that form right and straight angles, respectively. Since adjacent angles are two angles that share a common point and a common side, this means that there are instances that they form right or straight angles too. </p>
<ul><li>When two adjacent angles form a right angle and add up to 90<sup>o</sup>, they are also complementary angles.</li></ul>
<figure class="wp-block-image size-full"><img src="https://visualfractions.com/blog/wp-content/uploads/2021/12/adjacent-angles-that-are-also-complementary-angles.png" alt="" class="wp-image-369"/></figure>
<p>Similarly, when two adjacent angles form a straight angle and add up to 180<sup>o</sup>, they are also supplementary angles.</p>
<figure class="wp-block-image size-large"><img src="https://visualfractions.com/blog/wp-content/uploads/2021/12/adjacent-angles-that-are-also-supplementary-angles-1024x320.png" alt="" class="wp-image-367"/></figure>
<p>This means that when you see complementary or supplementary angles that share a common point and side, they are also adjacent angles. This statement remains true when reversed as well. For our last problem, we want you to work with complementary and supplementary adjacent angles and apply what you’ve just learned.</p>
<h3 class="wp-block-heading">Problem 3</h3>
<p>Angles [katex]\angle AOB and \angle BOC are adjacent angles that are complementary angles as well. What is the value of \angle AOB when \angle BOC = 70\degree?
First, try to sketch the diagram representing our problem. Make sure that the adjacent angles sketched will have a common point of O and a common side, \overline{OB}.
For two adjacent angles to be complementary, the sum of their angles must add up to 90o. This means that the larger angle, \angle AOC will have a sum of 90o. To find the measure of \angle BOC, simply subtract \angle AOB’s measure from 90o.
\begin{aligned}\angle AOB &= 90\degree - \angle BOC\\&= 90\degree – 70\degree \\&= 20\degree \end{aligned}This means that \angle AOB has a measure of 20o.
Problem 4
Angles \angle AOC and \angle BOC are adjacent angles that are supplementary angles as well. What is the value of \angle AOB when \angle BOC = 60\degree?
This problem is similar to our previous one, but this time, we’re working with adjacent angles that are supplementary. Meaning, the two angles will form a linear angle and will add up to 180o. Sketch a diagram to help guide you solve this problem.
This means that \angle AOB has an angle measure of 180o and is a straight line. To find the measure of \angle AOB, we subtract \angle AOC’s measure from 180o.
\begin{aligned}\angle AOC &= 180\degree - \angle BOC\\&= 180\degree – 60\degree \\&= 120\degree \end{aligned}Hence, \angle AOC has a measure of 120o.
