90 Degree Clockwise Rotation – Visual Fractions

The 90-degree clockwise rotation is a special type of rotation that turns the point or a graph a quarter to the right. When given a coordinate point or a figure on the xy-plane, the 90-degree clockwise rotation will switch the places of the x and y-coordinates: from $(x, y)$ to $(y, -x)$ .

Knowing how rotate figures in a 90 degree clockwise rotation will simplify the process of graphing and transforming functions. This rotation is one of the most common transformations, so it’s a helpful toolkit to add when working with more complex graphs. In this article, we’ll show you how easy it is to perform this rotation and show you techniques to remember to master rotating figures in a 90-degree clockwise direction.

What Is a 90 Degree Clockwise Rotation?

The 90-degree clockwise rotation represents the movement of a point or a figure with respect to the origin, $(0, 0)$ . In a 90 degree clockwise rotation, the point of a given figure’s points is turned in a clockwise direction with respect to the fixed point. The origin is the rotation’s fixed point unless stated otherwise.

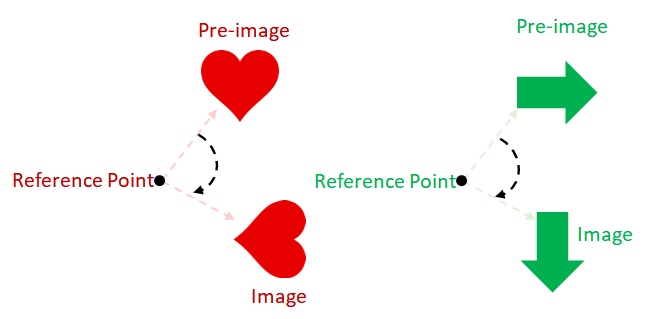
In a coordinate plane, when the point $(x, y)$ is rotated in a 90-degree clockwise direction, the projected image will have a coordinate of $(y, -x)$ . This also means that when a figure is rotated in the same direction on a Cartesian plane, all the points will exhibit the same behavior.

Original Point (Pre-image)	Rotated Point (Image)
$\begin{aligned}(x, y)\end{aligned}$	$\begin{aligned}(y, -x)\end{aligned}$

To better understand how the 90 degree clockwise rotation works, let’s take a look at the rotations for the following figures: $A \rightarrow A^{\prime}$ and $\Delta ABC \rightarrow A^{\prime}B^{\prime} C^{\prime}$ . When working on rotations, always refer to the fixed point when turning the pre-image (the original figure) to form the resulting image of the transformation.

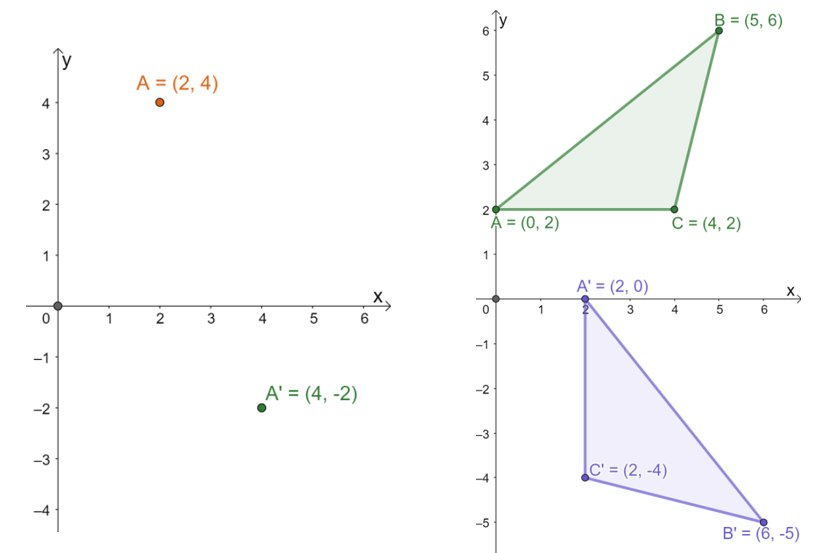
First, focus on how the point, $A$ , is rotated in a 90 degree clockwise direction with the origin placed as its reference point. Construct two rays by connecting the origin to the pre-image and the resulting image. We can see that the two rays, $\overrightarrow{OA}$ and $\overrightarrow{OA^{\prime}}$ , form a right angle. This confirms that point A was rotated about 90o in a clockwise direction to reach the projected point, $A^{\prime}$ .

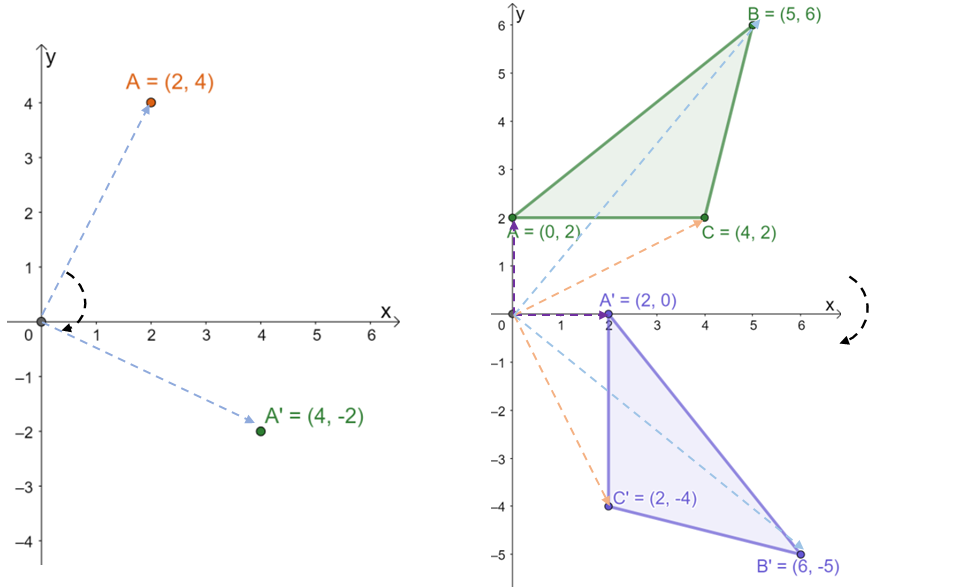
Now, focus on the transformation of $\Delta ABC$ and observe the angles formed by the rays from the following three pairs of points: $A \rightarrow A^{\prime}$ , $B \rightarrow B^{\prime}$ , and $C\rightarrow C^{\prime}$ .

$\overrightarrow{OA}$ and $\overrightarrow{OA^{\prime}}$ form a right angle.
$\overrightarrow{OB}$ and $\overrightarrow{OB^{\prime}}$ are also perpendicular to each other.
$\overrightarrow{OC}$ and $\overrightarrow{OC^{\prime}}$ also form a 90^o angle.

All three rotations are in a clockwise direction, so we can confirm that $\Delta A^{\prime}B^{\prime}C^{\prime}$ is the result when $\Delta ABC$ is rotated at a right angle and in a clockwise direction. Now, it’s time to observe how the significant points’ coordinates behave after rotating the two figures.

90 Degree Clockwise Direction
$\begin{aligned}A \rightarrow A^{\prime}\end{aligned}$	$\begin{aligned}(2, 4) \rightarrow (4, -2)\end{aligned}$
$\begin{aligned}\Delta ABC \rightarrow \Delta A^{\prime}B^{\prime}C^{\prime}\end{aligned}$	$\begin{aligned}A: (2, 4) \rightarrow (4, -2)\\B: (5, 6) \rightarrow (6, -5)\\C: (4, 2) \rightarrow (2, -4)\end{aligned}$

These transformations on the core points confirm that when rotating a point or a figure in a 90 degree clockwise direction, the x and y-coordinates switch their places, where the new y-coordinate is the negative equivalent of the pre-image’s x-coordinate – $P: (x, y) \rightarrow P^{\prime}: (y, -x)$ .

Problem 1

The four points and their corresponding rotations are graphed on the Cartesian plane shown below.

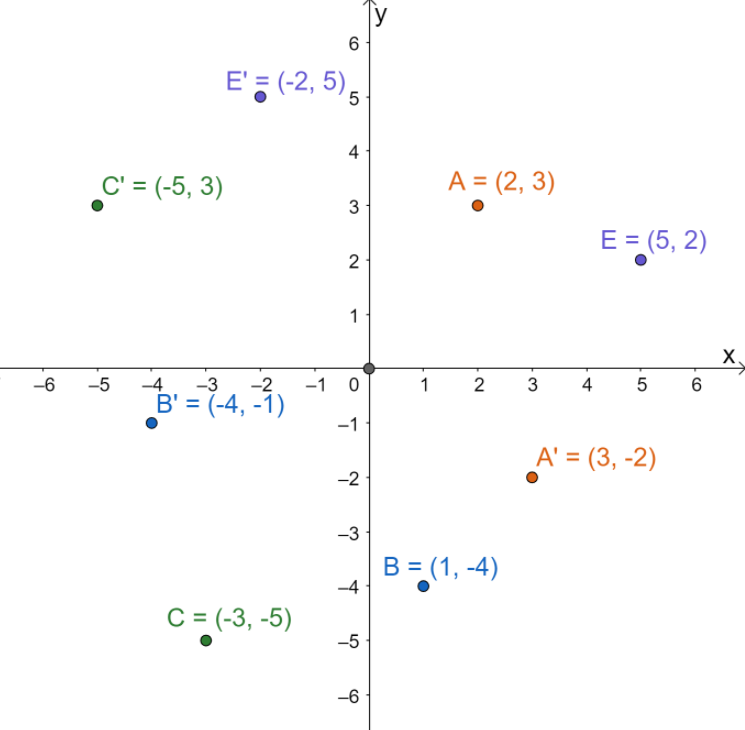
Which of the following points do not reflect a 90-degree clockwise rotation?

A. $A\rightarrow A^{\prime}$

B. $B\rightarrow B^{\prime}$

C. $C\rightarrow C^{\prime}$

D. $E\rightarrow E^{\prime}$

There are two ways to confirm the rotation performed on each of the pair of pre-image and image points. We can do this by measuring the angle formed by the rays connecting the origin and pairs of points.

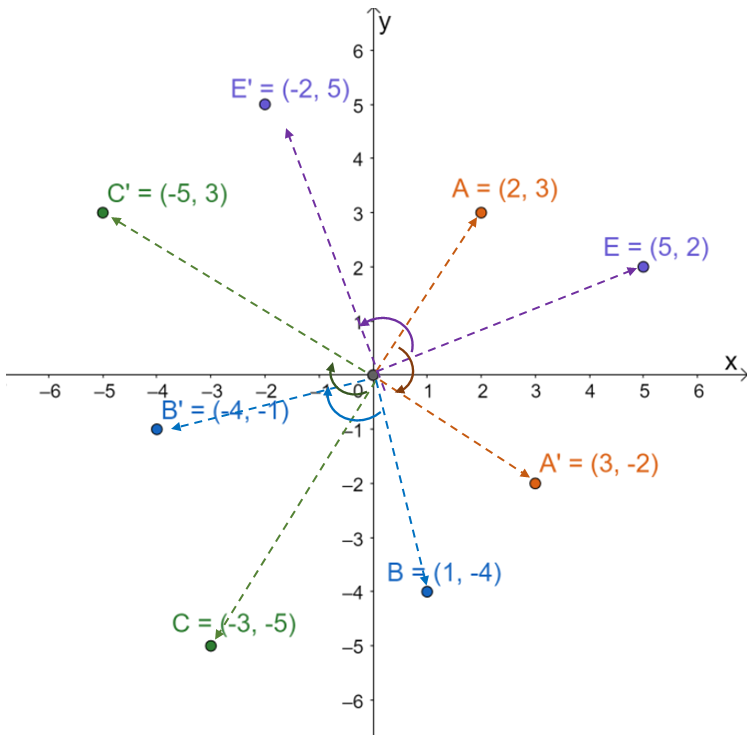
By quickly scanning the angles formed by the four pairs of points, we can see that they all form angles close to 90^o. This is an approximation since we’re just inspecting the angles. To confirm that these angles measure 90^o, use a compass and see if the angle formed by each pair of points form a right angle. Now, observe the direction of the rotation.

The following rotations are turned in a clockwise direction: $A \rightarrow A^{\prime}$ , $B \rightarrow B^{\prime}$ , and $C \rightarrow C^{\prime}$ .
Meanwhile, for $E \rightarrow E^{\prime}$ , the pre-image is turned 90 degrees in a counterclockwise direction.

This means that the rotation, $E \rightarrow E^{\prime}$ , does not exhibit the 90 degree clockwise rotation but instead, it is the result of rotating $E$ in a 90-degree counterclockwise direction and still with respect to the origin.

A more accurate way of confirming the rotations of this point is by observing their x and y-coordinates.

$\begin{aligned}A \rightarrow A^{\prime}\end{aligned}$	$\begin{aligned}(2, 3) \rightarrow (3, -2)\end{aligned}$
$\begin{aligned}B \rightarrow A^{\prime}\end{aligned}$	$\begin{aligned}(1, -4) \rightarrow (-4, -1)\end{aligned}$
$\begin{aligned}C \rightarrow C^{\prime}\end{aligned}$	$\begin{aligned}(2, 3) \rightarrow (3, -2)\end{aligned}$
$\begin{aligned}E\rightarrow E^{\prime}\end{aligned}$	$\begin{aligned}(5, 2) \rightarrow (-2, 5)\end{aligned}$

By observing the effect of the rotation on each of the resulting images of the four points, we can see that the first three rotations exhibit what we expect from a 90 degree clockwise rotation: $(x, y) \rightarrow (y, -x)$ . Meanwhile, for the fourth point, $(5, 2) \rightarrow (-2, 5)$ , the coordinates do not exhibit this behavior. Instead, this is how we expect the coordinates of a point will behave when turned 90 degrees in a counterclockwise rotation. Hence, the correct answer is D: $E\rightarrow E^{\prime}$ .

Now, what if we’re given the figure to rotate in a 90-degree clockwise direction? We’ll show you how in the next section!

How To Transform a Figure in a 90 Degree Clockwise Rotation?

There are two ways to transform a figure in a 90 degree clockwise rotation: 1) use a compass and a straightedge to accurately project the image of a figure and 2) project the x and y-coordinates of the figure when it is on a xy-plane: $(x, y) \rightarrow (y, -x)$ .

To decide which method would best work for a given problem, observe what’s given. If the figure being rotated is outside a Cartesian plane, use the first method to accurately graph the projected image. Now, if we’re given a figure graphed on a Cartesian plane, the second method is a much simpler approach.

In the next problems, we’ll show different examples of applying the second method. When ready, try to work on the problems we’ve prepared just for you!

Problem 2

Predict the result when the pre-image (the pizza) is rotated in a 90-degree clockwise direction with respect to the reference point as shown below.

The goal here is to have an idea of the resulting position of the image after being rotated 90 degrees in a clockwise direction. To do this, construct the first ray by connecting the reference point to the object.

Construct the second ray of the angle by creating a right angle (angle measuring 90o), so the two line segments must form an “L”-shape and is going to the right of the first ray. We do this so that the clockwise direction is accounted for.

Project the pre-image of the pizza and follow the direction as a guide in rotating the pizza in a 90 degree clockwise rotation. Observe how the pizza rotated to better understand how images are formed after being rotated 90 degrees clockwise.

Problem 3

What are the vertices of the projected image after $\Delta ABC$ is rotated 90 degrees and in a clockwise direction? Extend the xy-plane shown below then graph the rotated image of $\Delta ABC$ .

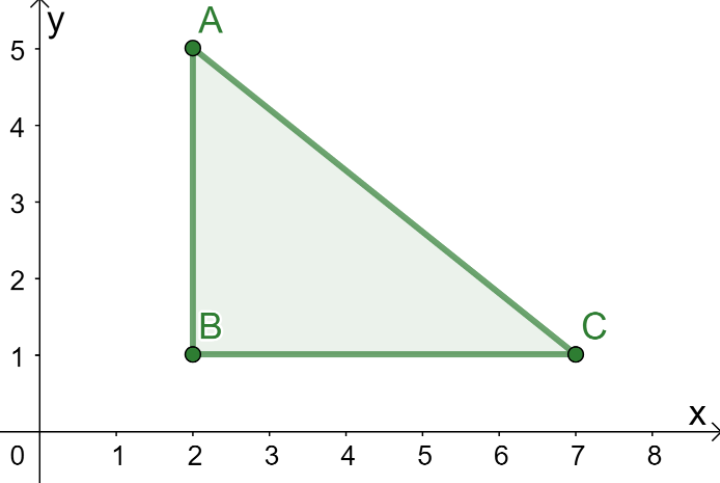
Now that the image we’re rotating is graphed on a xy-plane, take note of the figure’s key points first. For $\Delta ABC$ , its key points are its vertices: $A= (2, 5)$ , $B= (1, 1)$ , and $A= (7, 1)$ . To reflect the triangle, reflect these three vertices first by applying the rule for 90 degree clockwise rotation: $(x, y) \rightarrow (y, -x)$ .

$\begin{aligned}\boldsymbol{(x, y) \rightarrow (y, -x)} \end{aligned}$
$\begin{aligned}A\rightarrow A^{\prime}\end{aligned}$	$\begin{aligned}(2, 5) \rightarrow (5,-2)\end{aligned}$
$\begin{aligned}B\rightarrow B^{\prime}\end{aligned}$	$\begin{aligned}(1, 1) \rightarrow (1,-1)\end{aligned}$
$\begin{aligned}C\rightarrow C^{\prime}\end{aligned}$	$\begin{aligned}(7, 1) \rightarrow (1,-7)\end{aligned}$

The table summarizes the new vertices of our triangle. Now, let’s plot the three rotated vertices on the xy-plane then connect them to form the image of the triangle, $A^{\prime}B^{\prime}C^{\prime}$ .