The 3-4-5 right triangles are special right triangles that exhibit a unique Pythagorean triple for their side lengths ratio. Knowing what makes these triangles special will simplify the process of solving right triangles’ measures and word problems involving these triangles. The 3-4-5 right triangles will also help refresh your understanding of the Pythagorean theorem and triples.
In this article, understand the properties that define 3-4-5 right triangles and learn how to identify these triangles by inspecting their sides. Explore the different problems involving 3-4-5 right triangles and know their properties by heart here. Feel confident when working with these triangles by the end of this discussion!
What Is a 3 4 5 Right Triangle?
The 3-4-5 triangle is a special type of right triangle with side lengths sharing a specific ratio: 3:4:5, where the third component represents the length of its hypotenuse. Since the right triangle will always have this special ratio, all 3-4-5 triangles will always have three different integer side lengths. This means that 3-4-5 right triangles are scalene right triangles.
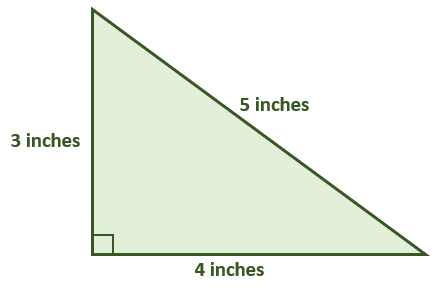
The most basic 3-4-5 triangle is the right triangle with the following side lengths: 3 inches, 4 inches, and 5 inches. All right triangles will satisfy the Pythagorean theorem, so the 3-4-5 right triangle is no exception. The Pythagorean theorem states that the sum of the sides’ squares must be equal to the square of the right triangle’s hypotenuse.
\begin{aligned}a^2 + b^2 &= c^2\\ (3)^2 + (4)^2 &= (5)^2\\ 9 +16&= 25\\25 &\overset{\checkmark}{=} 25 \end{aligned}As expected, the right triangle shown above satisfies the Pythagorean theorem. This is true for all 3-4-5 right triangles. As long as the sides of a scalene right triangle reduce to a ratio of 3:4:5, the triangle is a 3-4-5 right triangle. Before generalizing the process of finding these triangles, take a look at the right triangle shown below first.
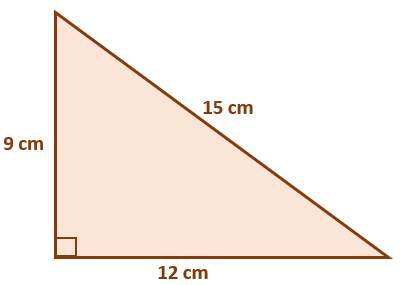
Observe the side lengths of the right triangle: 9 cm, 12 cm, and 15 cm. Write down the ratio of the sides then simplify to see if it is also a 3-4-5 right triangle.
9 : 12: 15 = 3: 4 : 5By simplifying the ratio of the triangle’s side, we can confirm that the triangle is indeed a 3-4-5 right triangle. As expected, this 3-4-5 right triangle also satisfies the Pythagorean theorem.
\begin{aligned}a^2 + b^2 &= c^2\\ (9)^2 + (12)^2 &= (15)^2\\ 81 +144&= 225\\225 &\overset{\checkmark}{=} 225 \end{aligned}In fact, all 3-4-5 right triangles showcase side lengths that are Pythagorean triples. This means that knowing why and how to identify Pythagorean triples is helpful when working with 3-4-5 right triangles.
Pythagorean Triples and 3 4 5 Right Triangles
The side lengths of a 3-4-5 right triangle are always Pythagorean triples– these are set of integers that satisfy the Pythagorean theorem. Similar to other Pythagorean triples, the multiples of the set, \{3, 4, 5\}, will also be side lengths of 3-4-5 right triangles. This means that when a right triangle has any of these Pythagorean triples, it is going to be a 3-4-5 right triangle.
| Pythagorean Triples | ||
| {3, 4, 5} | {6, 8, 10} | {9, 12, 15} |
| {12, 16, 20} | {15, 20, 25} | {18, 24, 30} |
| {21, 28, 35} | {24, 32, 40} | {27, 36, 45} |
This table can go on endlessly since any factor can be multiplied to each of the values from {3, 4, 5} to form a new set of a Pythagorean triple. Suppose that n is a positive factor, the Pythagorean triple, \{3n, 4n, 5n\} represents the sides of a 3-4-5 right triangle.

The triangle shown above is the general form of the 3-4-5 right triangle. As with all right triangles, the general form satisfies the Pythagorean theorem as well. Substitute these side lengths in terms of n into the Pythagorean theorem’s equation.
\begin{aligned}a^2 + b^2 &= c^2\\ (3n)^2 + (4n)^2 &= (5n)^2\\ 9n^2 +16n^2 &= 25n^2\\25n^2 &\overset{\checkmark}{=} 25n^2 \end{aligned}This confirms that the side lengths of any 3-4-5 right triangle will always be a Pythagorean theorem. In addition, we can find different side lengths for a 3-4-5 right triangle by multiplying the Pythagorean triple, {3, 4, 5}, by a positive integer.
Problem 1
Apply what you’ve learned in this section to identify the 3-4-5 right triangles among the five right triangles shown below.
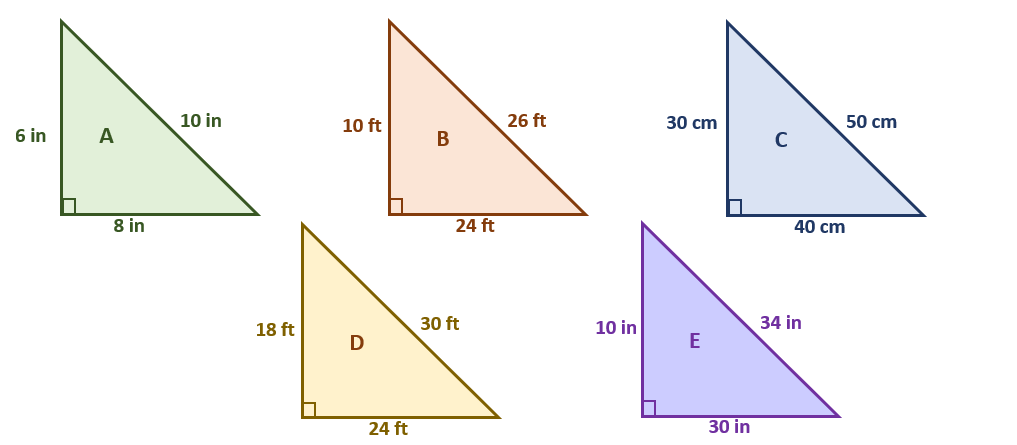
To confirm that a given right triangle is a 3-4-5 right triangle, find the ratios of the side lengths then see if they reduce to 3:4:5. If the ratio reduces to 3:4:5, we can confirm that the triangle is indeed a 3-4-5 right triangle. The table below summarizes the side length ratios of the five triangles.
| Triangle A | 6:8:10 = 3:4:5 |
| Triangle B | 10:24:26 = 5:12:13 |
| Triangle C | 30: 40:50 = 3:4:5 |
| Triangle D | 18 :24:30 = 3: 4 :5 |
| Triangle E | 10:30:34 = 5:15:17 |
There are only two triangles with side length ratios not equal to 3:4:5 – these are triangles B and E. This means that the remaining triangles are 3-4-5 right triangles. Hence, triangles A, C, and D are all 3-4-5 right triangles. Now that we’ve established the rules for identifying 3-4-5 right triangles, it’s time to expand our understanding and learn how to apply them when solving unknown measures and problems.
How To Solve 3 4 5 Right Triangle Problems?
Utilize the common ratio that 3-4-5 right triangles share when solving problems involving them. When looking for an unknown measure of a 3-4-5 right triangle, identify the side that corresponds with the ratio’s component. Simplify the process of solving problems by utilizing the Pythagorean triple, {3, 4,5}, and its corresponding multiples.
In this section, we’ll cover some examples showing how helpful 3-4-5 right triangles can be when solving problems. When dealing with 3-4-5 right triangles, knowing their properties will make a difference. Here are the properties of 3-4-5 right triangles that will come in handy later on:
- The 3-4-5 right triangles will always have three unequal sides that share a common ratio of 3:4:5.
- The three side lengths of 3-4-5 right triangles will always be Pythagorean triples that are multiples of {3, 4, 5}.
- All 3-4-5 right triangles will have interior angles with measures of 36.87o, 53.13o, and 90o.
Utilizing these properties simplifies the steps for solving unknown measures of a right triangle. Learn how without using Pythagorean’s theorem, it’s still possible to solve and work with these special right triangles.
Problem 2
A right triangle has a leg that measures 48 cm and a hypotenuse that is 80 cm long. What is the length of the right triangle’s remaining leg?
When working with problems like this, the first thing to do is to confirm that we’re working with a 3-4-5 right triangle. To do so, find the ratio of the two remaining sides to see if they simply to two components of 3:4:5 with 80 cm corresponding to the third ratio component.

Let h be the unknown leg of the right triangle, so the ratio of the right triangle’s side lengths is h: 48: 80. When simplified, the ratio of the three sides becomes h/16 : 3: 5. This crosses off our condition – the simplified ratio must have at least two components of 3: 4: 5.
h: 48: 80 = \dfrac{h}{16}: 3: 5Rearranging the ratio of the right triangle’s side lengths, we have 3: h/16 : 5. This means that the unknown leg represents the 3-4-5 right triangle’s side that is a multiple of 4. To find the value of h, simply equate h/16 to 4.
\begin{aligned}\dfrac{h}{16} &= 4\\h &= 4(16)\\ h&= 64\end{aligned}This means that the unknown leg’s length is 64 cm. We can confirm this by seeing if the side lengths reduce to 3:4:5.
\begin{aligned}48: 64:80 = 3: 4: 5\end{aligned}Problem 3
A rectangle is formed by two right triangles as shown below. What is the diagonal of the rectangle?
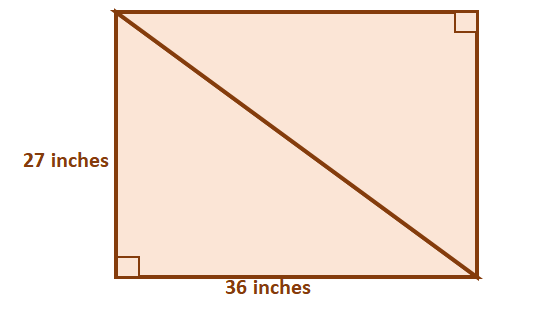
The diagonal of the rectangle is also the hypotenuse of each of the right triangles. Now, let h represent the hypotenuse of the right triangle. Observe the ratio of the right triangle’s sides first to see if we can apply the properties of 3-4-5 triangles for this problem.
27: 36: h = 3: 4: hSince the legs of the right triangle have side lengths with a ratio of 3:4, we’re working with a 3-4-5 right triangle. The common factor shared between the legs is 9, so h must also share this as a common factor along with 5 as another factor.
\begin{aligned}h &= 9(5)\\&= 45\end{aligned}This means that the value of h is equal to 45 inches. We can also confirm this by simplifying 27:36:45 – it returns a ratio of 3:4:5. Hence, the diagonal of the rectangle is also 45 inches long.
