Solving single-step inequalities (also known as one-step inequalities) is an essential skillset that you need to equip yourself within algebra. This paves the way to knowing how to simplify and solve more complex inequalities that you’ll encounter later on in your more advanced math classes.
In this article, learn how to solve single-step inequalities using the four arithmetic operations: addition, subtraction, multiplication, and division. Learn how to assess inequalities to know the best method to use when solving any inequality. You’ll also have the chance to test your understanding as we’ve prepared a wide range of examples just for you!
How To Solve Single-step Inequalities?
When solving single-step inequalities, the goal is to isolate the variable on one end of the inequality. There are four possible methods when solving single-step inequalities: 1) by addition, 2) by subtraction, 3) by multiplication, and 4) by division.
In the past, you’ve learned that inequalities are algebraic expressions that relate two or more unequal quantities. These are the four inequalities that you should be familiar with by now:
- m < n: this inequality indicates that the value of m is less than n
- m ≤ n: this inequality indicates that the value of m is less than or equal to n
- m > n: this inequality indicates that the value of m is greater than n
- m ≥ n: this inequality indicates that the value of m is less than or equal to n
There are instances, however, that the inequalities are still not simplified and need to be solved so that we know the inequality’s solution. When this happens, it is important that you know how to use different algebraic techniques to solve the inequality. There are a plethora of inequalities available and each inequality requires a unique process for it to be solved.
This is why having a strong foundation for solving fundamental inequality types is essential. Our discussion focuses on solving different single-step inequalities using different arithmetic operations.
| Solving Single-step Inequality by Addition | \begin{aligned}x - 1 &< 5\\x -1\,{\color{Purple}+1} &< 5 \,{\color{Purple}+1}\\x &< 6\end{aligned} |
| Solving Single-step Inequality by Subtraction | \begin{aligned}x + 4 &> -6\\x+4\,{\color{DarkOrange}-4} &> -6 \,{\color{DarkOrange}-4}\\x &> -10\end{aligned} |
| Solving Single-step Inequality by Multiplication | \begin{aligned}\dfrac{1}{3}x &\leq -2\\\dfrac{1}{3}x\,{\color{Green}\cdot \,3} &\leq -2{\color{Green}\cdot \,3}\\x &\leq -6\end{aligned} |
| Solving Single-step Inequality by Division | \begin{aligned}5x &\geq 10\\\dfrac{5x}{\color{Blue}5} &\geq \dfrac{10}{\color{Blue}5}\\x &\geq 2\end{aligned} |
Don’t worry, you’ll get a chance to work on different types of single-step inequalities in this article. For now, what’s important is for you to understand why these inequalities are called single-step inequalities. Observe the process of solving each inequality, what do you see? For each inequality, you are required to only perform one arithmetic operation to find its solution. This is what makes single-step inequalities special!
How To Solve Single-step Inequalities by Addition?
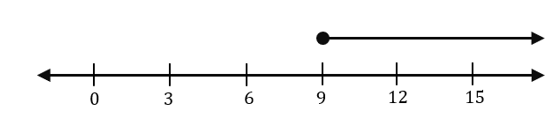
When using addition to solve a single-step inequality, add both sides of the equation by a constant that isolates the inequality’s variable. For example, when working with the inequality, x – 1 < 5, the goal is to add a constant on the left-hand side of the inequality so x is isolated.
\begin{aligned}x - 1 &< 5\\x -1\,{\color{Purple}+1} &< 5 \,{\color{Purple}+1}\\x &< 6\end{aligned}From the worked-out solution, this confirms that adding 1 to both sides of the inequality isolates x to the left-hand side. This means that the solution to the inequality is equal to x < 6 or in interval notation, that’s (-\infty, 6).

The number line above highlights the solution to the single-step inequality as well. To generalize this rule for all single-step inequalities that can be solved by addition, we have the following shown below:
\begin{aligned}x - h &< k\\x -h\,{\color{Purple}+k} &< h \,{\color{Purple}+k}\\x &< h + k\end{aligned}This means that when given an inequality of the form, x -h <k, its solution is equal to x< h+k. Replace the inequality symbol by the three remaining ones and the rule still apply.
\begin{aligned}x - h \leq k&\Rightarrow x\leq h+k\\x - h > k&\Rightarrow x>h+k\\x - h \geq k&\Rightarrow x\geq h+k\end{aligned}Of course, the best way to master this process is through practice, so we’ve prepared some exercises for you to work on!
Problem 1
Find the solution to the following single-step inequalities.
a. x – 10 < 6
When given a single-step inequality such as the one shown above, the crucial part of the process is adding the right constant. Since the left-hand side of the inequality shows x - 10, add 10 to both sides of the inequality and see what happens.
\begin{aligned}x - 10 &< 6\\x -10\,{\color{Purple}+10} &< 6 \,{\color{Purple}+10}\\x &< 16\end{aligned}By adding 10 to both sides of the inequality, we now have its solution: x < 16 or (-\infty, 16). Here’s the number line representing the solution as well:

b. x – 2 \geq -3.5
Now, apply similar process to find the solution to this single-step inequality. The only difference is that the inequality used is ≥ (greater than or equal to). This means that in order to find the inequality’s solution, add 2 to both sides of the inequality.
\begin{aligned}x - 2 &\geq -3.5\\x -2\,{\color{Purple}+2} &\geq-3.5 \,{\color{Purple}+2}\\x &\geq -1.5\end{aligned}Hence, the solution to this single-step inequality is x \geq -1.5 or [-1.5, \infty). To help you understand the values covered by the solution, take a look at the number line below.

c. 3\pi > x - \pi
The third inequality may appear intimidating at first, but it becomes easier when you remind your self that π is simply a constant. Unlike the previous examples, the variable is now on the right-hand side of the inequality. Don’t worry, the process remains the same though. To solve the inequality, add π to both sides.
\begin{aligned}3\pi &> x-\pi\\3\pi \,{\color{Purple}+3\pi} &> x- \pi \,{\color{Purple}+\pi}\\6\pi &>x\end{aligned}This means that the solution to the inequality is 6\pi > x or when rearranged to the standard form, x < 6\pi. In interval notation, that’s equal to (-\infty, 6\pi).

Use these three examples to help guide you in solving other single-step inequalities. Always remember that the end-goal of single-step inequalities is to isolate the variable in one side of the inequality. In fact, solving single-step inequalities using addition and subtraction follow the same process. You’ll learn why in the next section.
How To Solve Single-step Inequalities by Subtraction?
To solve single-step inequalities by subtraction, the goal is to subtract both sides of the inequality by the constant beside the variable. Single-step inequalities that can be solved by subtraction normally contain x + h on either side of the inequality. This is why subtracting the constant, h, from both sides of the equation makes sense for inequalities like this.
\begin{aligned}x + 4 &> -6\\x+4\,{\color{DarkOrange}-4} &> -6 \,{\color{DarkOrange}-4}\\x &> -10\end{aligned}Just take a look at the earlier example for this method. Since the inequality contains x + 4 on its left-hand side, find its solution by subtracting 4 from both sides of the inequality. This shows that the inequality’s solution is x > -10 or (-10, \infty).

As with the previous section, why don’t we summarize the process for all four types of inequalities? The rule remains the same – simply subtract the right constant from both sides of the inequality to find its solution by subtraction.
\begin{aligned}x + h < k&\Rightarrow x< k -h\\x + h \leq k&\Rightarrow x\leq k -h\\x + h > k&\Rightarrow x>k -h\\x + h \geq k&\Rightarrow x\geq k -h\end{aligned}Use what you’ve just learned to solve the three inequalities shown below by subtracting the appropriate constant from both sides of the inequality.
Problem 2
Find the solution to the following single-step inequalities.
a. x + 10 < 8
Since the left-hand side of the inequality contains x + 10, subtract 10 from both sides of the inequality. This isolates the variable on one side and leads to the inequality’s solution.
\begin{aligned}x + 10 &> 8\\x+10\,{\color{DarkOrange}-10} &> 8\,{\color{DarkOrange}-10}\\x &> -2\end{aligned}This means that the solution to the single-step inequality is x > -2 or (-2, \infty). The number line to the inequality’s solution is as shown below.

b. x + \frac{2}{3} \geq 2
Apply a similar process to solve the second inequality. Subtract both sides of the equation by 2/3 to solve for the single-step inequality.
\begin{aligned}x +2/3 &\geq 2\\x+ 2/3\,{\color{DarkOrange}-2/3} &\geq 2\,{\color{DarkOrange}-2/3}\\x &\geq 4/3\end{aligned}
Hence, the solution to this inequality is x \geq \frac{4}{3} or [2/3, \infty). Take a look at the number line shown below to better understand the solution set for this inequality.

c. -1.5 \leq x + 2.5
Take a look at the right-hand side of the inequality: x + 2.5. To isolate the expression on the right-hand side by subtracting 2.5 from both sides of the equation.
\begin{aligned}-1.5 &\leq x +2.5\\-1.5\,{\color{DarkOrange}-2.5} &\leq x +2.5\,{\color{DarkOrange}-2.5}\\-4 &\leq x\end{aligned}From this, we can see that -4 \leq x or x \geq -4. The interval notation for this solution is also [-4, \infty) . Here’s the number line represent the solution set as well:

This wraps up the section for solving single-step inequalities by subtraction. Now, learn how to solve single-step inequalities that involve coefficients- both whole number and rational coefficients.
How To Solve Single-step Inequalities by Multiplication?
When solving single-step inequalities by multiplication, multiply both sides of the inequality by a constant that removes any coefficient before the variable. This method is most helpful when solving inequalities with rational coefficients before their variables. To appreciate this method better, take a look at the earlier example we’ve shown you.
\begin{aligned}\dfrac{1}{3}x &\leq -2\\\dfrac{1}{3}x\,{\color{Green}\cdot \,3} &\leq -2{\color{Green}\cdot \,3}\\x &\leq -6\end{aligned}By multiplying the reciprocal of the variable’s rational coefficient on both sides of the equation, the variable is now isolated. This leads to the actual solution of single-step inequality. Here are additional examples to help you understand this process better:
| \begin{aligned}\dfrac{1}{4}x &< 3\\\dfrac{1}{4}x\,{\color{Green}\cdot \,4} &< 3{\color{Green}\cdot \,4}\\x &<12\end{aligned} | \begin{aligned}\dfrac{2}{3}x &\geq -2\\\dfrac{2}{3}x\,{\color{Green}\cdot \,\dfrac{3}{2}} &\geq -2{\color{Green}\cdot \,\dfrac{3}{2}}\\x &\geq -3\end{aligned} | \begin{aligned}\dfrac{1}{5}x &> \dfrac{3}{10}\\\dfrac{1}{5}x\,{\color{Green}\cdot \,5} &> \dfrac{3}{10}{\color{Green}\cdot \,5}\\x &>\dfrac{3}{2}\end{aligned} |
Now, apply what you’ve learned to solve the single-step inequalities that follow. Always remember, look for the reciprocal of the variable’s coefficient right away.
Problem 3
Find the solution to the following single-step inequalities.
a. \frac{1}{4}x > -2
To solve this single-step inequality, identify the reciprocal of the coefficient before the variable, x. Hence, multiply both sides of the inequality by 4/1 or 4. This cancels out the coefficient and isolates the variable completely.
\begin{aligned}\dfrac{1}{4}x &> -2\\\dfrac{1}{4}x\,{\color{Green}\cdot \,4} &> -2{\color{Green}\cdot \,4}\\x &>-8\end{aligned}This means that the solution to this inequality is x > -8 or (-8, \infty). Here’s the number line reflecting the solution set to the inequality as well.

b. -\frac{2}{5}x \leq -10
Perform a similar process to solve the inequality shown above by multiplication. Begin by inspecting the variable and finding its coefficient’s reciprocal. Since the reciprocal of -2/5 is -5/2, multiply both sides of the inequality by -5/2.
\begin{aligned}-\dfrac{2}{5}x &\leq -10\\-\dfrac{2}{5}x\,{\color{Green}\cdot \,-\dfrac{5}{2}} &\leq -10{\color{Green}\cdot \,-\dfrac{5}{2}}\\x &\geq 25\end{aligned}Why did the inequality change? Remember that when multiply a negative constant on both sides of an inequality, the inequality reverses. This is why the solution to the equation is equal to x \geq 25 or in interval notation, [25, \infty).

c. \frac{x}{6} \geq 2
Inspecting the left-hand side of the inequality, we have x/6, so the coefficient of the variable is 1/6. This means that for us to solve this single-step inequality, we have to multiply both sides of the equation by 6.
\begin{aligned}\dfrac{x}{6} &\geq 2\\\dfrac{x}{6}\,{\color{Green}\cdot \,6} &\geq 2{\color{Green}\cdot \,6}\\x &\geq 12\end{aligned}Hence, the solution to this inequality is x \geq 12 or [12, \infty). Take a look at the number line of the inequality’s solution set as well.
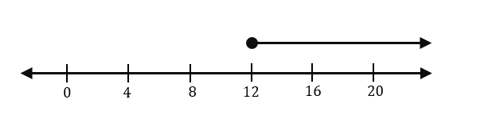
How To Solve Single-step Inequalities by Division?
When solving single-step inequalities by division, divide both sides of the equation by a constant that cancels out the coefficient before the variable. This method is used when the algebraic term is isolated on one side and contains coefficients that are greater than the absolute value of 1. Take a look at the single-step inequality shown below to better appreciate this method.
\begin{aligned}5x &\geq 10\\\dfrac{5x}{\color{Blue}5} &\geq \dfrac{10}{\color{Blue}5}\\x &\geq 2\end{aligned}We can see that by dividing both sides of the inequality by 5, we end up with the inequality’s solution set. Here are other examples of single-step inequalities that can be solved by division.
| \begin{aligned}6x &\leq 18\\\dfrac{6x}{\color{Blue}6} &\leq \dfrac{18}{\color{Blue}6}\\x &\leq 3\end{aligned} | \begin{aligned}-4x &> 2\\\dfrac{-4x}{\color{Blue}-4} &< \dfrac{2}{\color{Blue}-4}\\x &< -\dfrac{1}{2}\end{aligned} | \begin{aligned}1.5x &< 6\\\dfrac{1.5x}{\color{Blue}1.5} &< \dfrac{6}{\color{Blue}1.5}\\x &< 4\end{aligned} |
These three examples highlight how dividing the right coefficient on both sides of the equation will make solving these inequalities simpler for you. Don’t worry, you still have more exercises to try on!
Problem 4
Find the solution to the following single-step inequalities.
a. 24x \leq 144
Take a look at the left-hand side of the inequality – the coefficient before x is 24. This means that for us to find the solution to this single-step inequality, divide both sides of the inequality by 24.
\begin{aligned}24x &\leq 144\\\dfrac{24x}{\color{Blue}24} &\leq \dfrac{144}{\color{Blue}24}\\x &\leq 6\end{aligned}This means that the solution set to this inequality is x \leq 6 or (-\infty, 6].

To understand the values covered by this inequality, take a look at the number line of the solution set. Double-check the solution set by choosing a value within the set and see if the inequality remains.
\begin{aligned}24x &\leq 144\\24({\color{Blue}4}) &\leq 144\\ 96 &\overset{\checkmark}{\leq}144\end{aligned}b. 2.5x > 50
This time, the coefficient before x is a decimal. The process won’t change since the coefficient is still greater than 1. Hence, divide both sides of the inequality by 2.5 to solve the single-step inequality.
\begin{aligned}2.5x &>50\\\dfrac{2.5x}{{\color{Blue}2.5}}&> \dfrac{50}{{\color{Blue}2.5}}\\x &>20\end{aligned}Hence, the solution to the single-step inequality is x > 20 or (20, \infty).
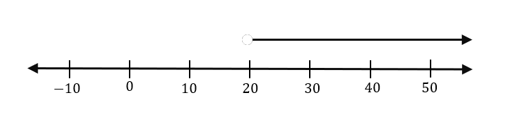
Use the number line to guide you in double-checking whether the solution set is correct. We’ll that for you to work on!
c. 36 \leq -4x
The variable may be on the right-hand side of the inequality, but the process remains the same. Now, the absolute value of -4 is equal to 4, so use division to solve the single-step inequality. Divide both sides of the inequality by -4 and switch ≤ to ≥ to account for dividing both sides of the inequality by a negative constant.
\begin{aligned}36 &\leq -4x\\\dfrac{36}{{\color{Blue}-4}}&\geq \dfrac{-4x}{{\color{Blue}-4}}\\9 &\geq x\end{aligned}This shows that the solution set to the inequality is 9 \geq x or x \leq 9. In interval notation, that’s (-\infty, 9]. Here’s the number line representing the solution set as well.